(아침산책)
# 문제
아침 산책을 즐기는 서현이는 서울과학고에 입학해서도 아침 산책을 즐기려고 합니다. 서현이는 산책을 위해 서울과학고의 지리를 분석했고, 그 결과 서울과학고를
$N$개의 장소를
$N-1$개의 길이 잇는 트리 형태로 단순화시킬 수 있었습니다. 트리 구조이므로, 모든 장소를 몇 개의 길을 통해 오고갈 수 있습니다.
아침 산책은 시작점과 도착점을 정하고, 시작점에서 도착점까지 트리 위의 단순 경로(같은 점을 여러 번 지나지 않는 경로)를 따라 걷게 됩니다. 트리 위의 두 점 사이의 경로는 유일하므로 시작점과 도착점이 정해지면 경로는 유일하게 결정됩니다.
$N$개 장소 중에 일부 장소는 실내이며, 나머지 장소는 실외입니다. 서현이는 산책을 시작하기 전부터 운동을 하는 것을 원치 않기 때문에, 산책의 시작점과 끝점은 모두 실내여야 합니다. 또한, 산책 도중에 실내 장소를 만나면 산책을 그만두고자 하는 욕구가 생기기 때문에, 산책 경로 위에 시작점과 끝점을 제외하고 실내 장소가 있으면 안 됩니다.
서현이는 매일 다른 산책 경로를 걷고자 합니다. 서로 다른 산책 경로가 몇 가지 있는지 구해 봅시다.
# 입력
첫 줄에는 정점의 수 $N$이 주어집니다.
둘째 줄에는 1과 0으로 이루어진 길이 $N$의 문자열 $A$가 주어집니다. $i$번째 문자 $A_i$가 1일 경우 $i$번 장소는 실내이며, 0인 경우 $i$번 장소는 실외입니다.
셋째 줄부터 $N+1$번 줄까지는 $i+2$번 줄에 트리의 각 간선을 나타내는 두 정수 $u_i$, $v_i$가 주어집니다. 이는 $i$번째 간선이 $u_i$번 정점과 $v_i$번 정점을 연결한다는 의미입니다.
# 출력
가능한 서로 다른 산책 경로의 수를 출력합니다.문제의 조건은 매우 간단합니다. 실내에서 시작하고 끝나는 경로를 찾으십시오.
얼마나 많은 야외 공간을 통과하는지에 대해 걱정할 필요가 없습니다. (실외 제로 거리도 가능!)
외출을 하는 경우와 외출을 하지 않는 경우를 알아보자!
야외를 지날 때
1. 야외 공간이 하나뿐인 경우
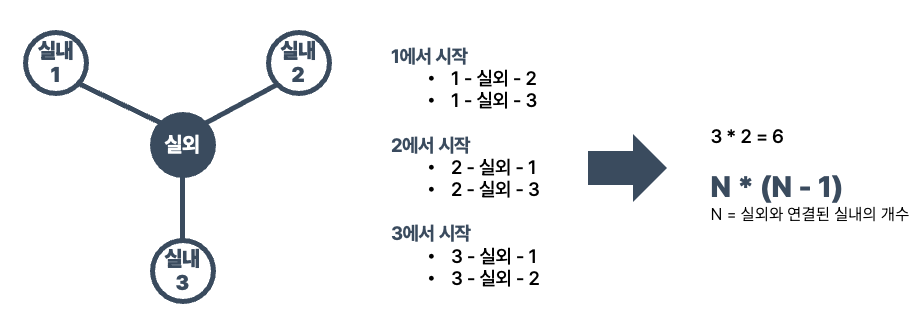
내부 정점을 시작점으로 하고 나머지 내부 정점 중 하나에 도달하면 경로가 끝납니다.
해당 정점이 없는 정점으로 이동하려면 시작 정점과 경우를 찾아야 합니다.
방의 수가 N일 때, N * (N-1)관련이 있을 수 있습니다
DFS 기능에서 인접한 내부 정점의 수계산 및 반환
def DFS(start):
visited(start) = True # 방문 처리
inside_count = 0 # 현재 노드와 인접한 실내 노드 개수를 저장할 변수
for v in graph(start):
# 인접한 노드가 실내라면
if inside(v) == '1':
inside_count += 1 # 실내 노드 개수 증가
return inside_count # 실내 노드 개수 반환
2. 실외기가 1대 이상인 경우
실외 공간을 연결하면 여러 개가 있어도 완전히 동일합니다.
자연을 얼마나 자주 걷는지는 중요하지 않기 때문입니다!
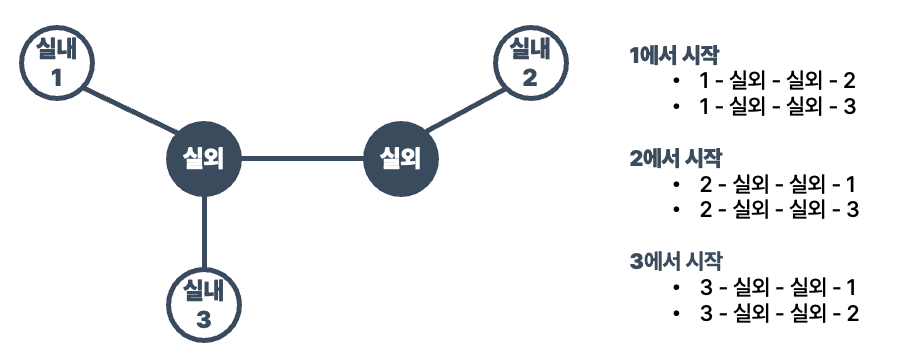
실외 노드에 인접한 노드를 검색하던 중 실외 노드를 발견하면
이 노드를 통과하고 이 외부 노드 옆에 있는 내부 공간의 수를 세어 더할 수 있습니다.
DFS 함수의 for문에 Outdoor의 경우 추가
# 인접한 노드가 실외라면
elif not visited(v) and inside(i) == "0": # 그 노드에서부터 탐색하여 실내 노드 개수 증가
inside_count += DFS(v)
자연이 연결되지 않는다면?!
3. 밖이 멀리 있을 때
자연이 멀리 있을 때
각 실외 공간과 인접한 실내 공간만 길을 찾으면 된다.
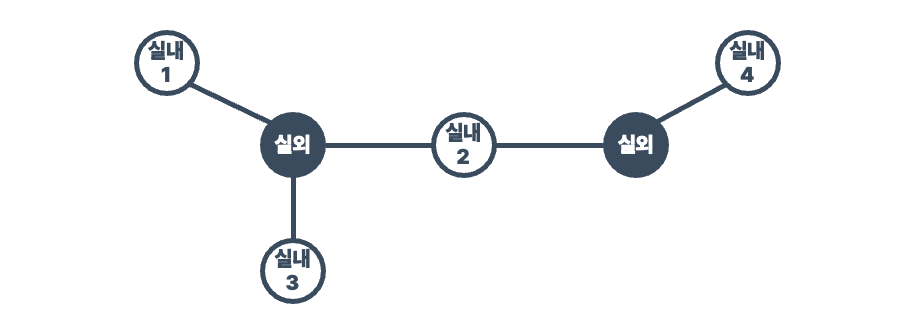
Indoor 2가 시작점이므로 각 Outdoor 옆에 Indoors가 공유됩니다.
실내2와 분리
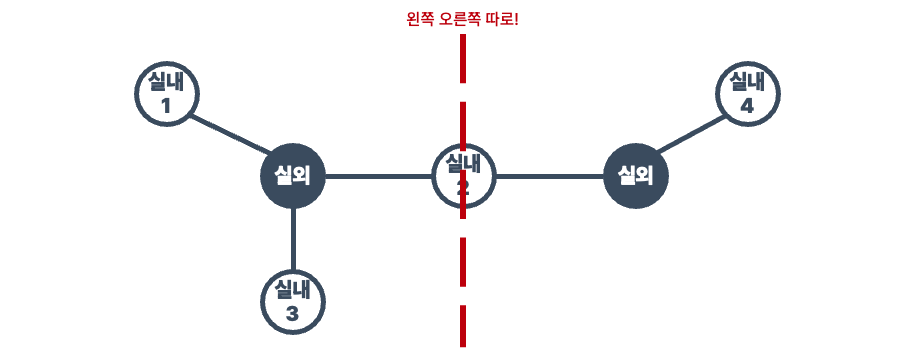
이 분할 차트에서는 이전과 같이 모든 경로를 검색하고 추가할 수 있습니다.
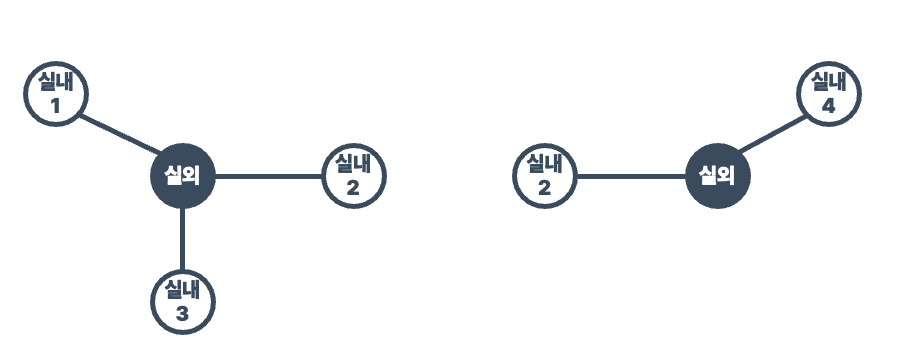
왼쪽에 3 * (3 - 1) = 6
오른쪽에 2 * (2 - 1) = 2
이 둘의 합 8그것은 개의 길로 밝혀졌습니다.
즉, 외부를 통한다면 1~3의 경우 모두 같다.
Outdoor에서 시작하여 Outdoor와 경계를 이루는 Indoor 노드의 수 N그냥 찾기 위해 N * (N-1)경로의 수를 찾기 위해.
위의 코드 1과 2를 결합하여 DFS 함수에서 반환한 실내 노드 수로 전체 경로 수를 계산하는 코드
def DFS(start):
visited(start) = True # 방문 처리
inside_count = 0 # 현재 노드와 인접한 실내 노드 개수를 저장할 변수
for v in graph(start):
# 인접한 노드가 실내라면
if inside(v) == '1':
inside_count += 1 # 실내 노드 개수 증가
# 인접한 노드가 실외라면
elif not visited(v) and inside(i) == "0": # 그 노드에서부터 탐색하여 실내 노드 개수 증가
inside_count += DFS(v)
return inside_count # 실내 노드 개수 반환
for i in range(1, N+1):
if inside(i) == '0' and not visited(i): # 시작이 실외일 때만 탐색
result = DFS(i) # DFS를 통해 인접한 실내 노드 개수를 계산
total += (result) * (result - 1) # 경로의 개수 추가
자연을 통하지 않는다면
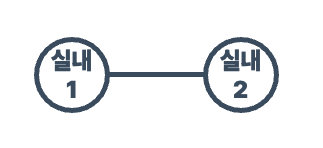
밖으로 나가지 않는다
그것은 실내에서 실내로 직접 이동합니다.
경로는 실내에서 만나면 끝납니다.
방에 인접한 모서리 점이 내부에 있는 경우에만 적용됩니다.
그리고 실내1 -> 실내2그리고 실내2 -> 실내1분리되어 있으므로 별도로 계산해야 합니다.
이 경우 회선 정보 수신 시
두 정점이 모두 내부에 있는 경우 총 경로 수 2추가하기만 하면 됩니다.
for _ in range(N-1):
a, b = map(int, sys.stdin.readline().split())
graph(a).append(b)
graph(b).append(a)
# 두 정점 모두 실내이면 경로의 수 2 증가
if inside(a) == "1" and inside(b) == "1":
total += 2
그만!
전체 코드
import sys
sys.setrecursionlimit(10**6)
N = int(input())
inside="0" + input() # 각 노드가 실내(1)인지 실외(0)인지 저장한 문자열
# 노드 번호를 index로 접근하기 위해 앞에 0 추가
graph = (() for _ in range(N+1))
visited = (False) * (N+1)
total = 0 # 경로의 개수를 저장할 변수
for _ in range(N-1):
a, b = map(int, sys.stdin.readline().split())
graph(a).append(b)
graph(b).append(a)
# 두 정점 모두 실내이면 경로의 수 2 증가
if inside(a) == "1" and inside(b) == "1":
total += 2
def DFS(start):
visited(start) = True # 방문 처리
inside_count = 0 # 현재 노드와 인접한 실내 노드 개수를 저장할 변수
for v in graph(start):
# 인접한 노드가 실내라면
if inside(v) == '1':
inside_count += 1 # 실내 노드 개수 증가
# 인접한 노드가 실외라면
elif not visited(v) and inside(i) == "0": # 그 노드에서부터 탐색하여 실내 노드 개수 증가
inside_count += DFS(v)
return inside_count # 실내 노드 개수 반환
for i in range(1, N+1):
if inside(i) == '0' and not visited(i): # 시작이 실외일 때만 탐색
result = DFS(i) # DFS를 통해 인접한 실내 노드 개수를 계산
total += (result) * (result - 1) # 경로의 개수 추가
print(total)


